Bridging Attention and State Space Models - A Systems Theory Perspective
Bridging Attention and State Space Models: A Systems Theory Perspective
In the rapidly evolving landscape of natural language processing, two major paradigms have shaped how we build language models: the Attention Mechanism that powers Transformers [2], and the recently revived State Space Models (SSMs) [3,4]. While these approaches seem fundamentally different at first glance, our recent work “Integrating the Attention Mechanism Into State Space Models”[1] presented at the IEEE Swiss Conference on Data Science reveals surprising connections and proposes a way to combine their strengths.

The Tale of Two Architectures
Attention Mechanisms: The Context Masters
The attention mechanism, popularized by the “Attention is All You Need” paper [2], works by allowing each token in a sequence to “look at” all previous tokens and decide which ones are most relevant for the current prediction.
Think of it like this: when you’re reading a sentence and trying to understand what “it” refers to, you automatically scan back through the text to find the most likely candidate. The attention mechanism does something similar - it computes similarity scores between tokens and uses these to create weighted combinations of past information.
Mathematically, for a token at position i, attention computes:
$$y_i = \sum_{j=1}^{i} a_{i,j} x_j W_V W_O$$
Where $a_{i,j}$ represents how much attention token i pays to token j, computed using query-key similarity:
$$a_{i,j} = \text{softmax}(x_j W_K W_Q^T x_i^T)$$
State Space Models: The Memory Keepers
State Space Models take a different approach. Instead of looking back at all previous tokens directly, they maintain a “memory state” that gets updated as each new token arrives. This state vector acts like a continuously updating summary of everything seen so far.
The SSM update equations are elegantly simple:
$$h_i = h_{i-1} A + x_i B \quad \text{(update memory)}$$
$$y_i = h_i C \quad \text{(generate output)}$$
Here, $h_i$ is the memory state, and matrices $A$, $B$, $C$ control how information flows through the system.
The Hidden Connection: Two Sides of the Same Coin
Here’s where something truly remarkable emerges from our analysis. Despite looking completely different on the surface, attention mechanisms and state space models are actually solving the same problem in surprisingly similar ways.
When we carefully expand the mathematical equations for both approaches, something amazing happens.

Both are saying: “Take each past token, multiply it by some weight, and add them all up.”
The profound realization is that both mechanisms are computing weighted averages of past information - they just calculate the weights differently:
- Attention weights ($W_{i,j}$): “How relevant is this past token to what I’m trying to understand right now?” (content-based)
- SSM weights ($V_{i,j}$): “How much should this past token influence me, given how long ago it was?” (position-based with exponential decay)
Think of it like this:
- Attention is like a smart librarian who picks the most relevant books for your research question, regardless of when they were written
- SSMs are like your memory - recent events are vivid and influential, while older memories fade gradually but systematically
Why does this matter?
This connection reveals that the attention vs. SSM debate isn’t about choosing completely different approaches - it’s about choosing different strategies for the same fundamental task: deciding how much weight to give to different pieces of past information.
Understanding this similarity opens up new possibilities: What if we could combine the best of both worlds? What if we could create systems that are both computationally efficient like SSMs AND contextually smart like attention?
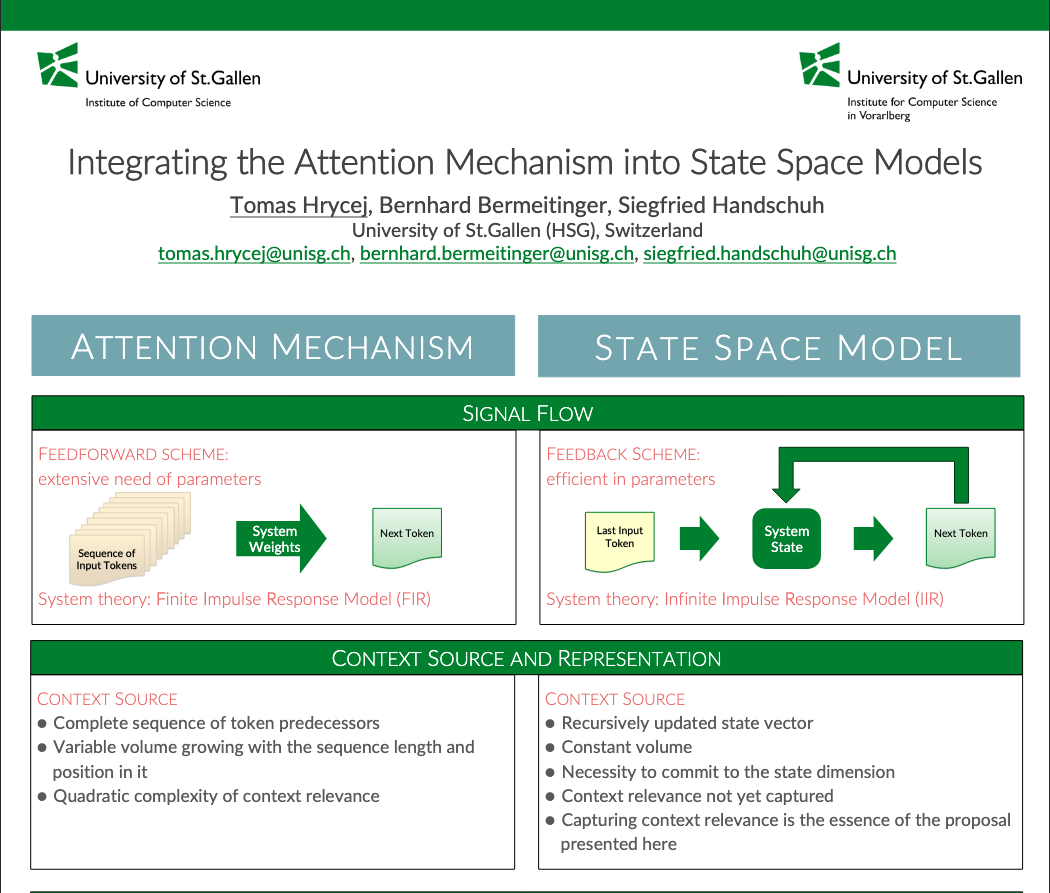
From a signal processing perspective:
- Attention behaves like a Finite Impulse Response (FIR) filter: It needs separate parameters for each possible input position
- SSMs behave like Infinite Impulse Response (IIR) filters: They use feedback and memory, making them more parameter-efficient
The Trade-off: Context vs Efficiency
This reveals the fundamental trade-off:
Attention’s Strength: Context Awareness
Attention excels at capturing which past tokens are contextually relevant, regardless of their position. If “John” appears 50 tokens back but is crucial for understanding the current sentence, attention can focus on it directly.
SSM’s Strength: Computational Efficiency
SSMs process sequences in linear time and use far fewer parameters. Their memory state provides a compact summary of the entire past sequence, making them ideal for very long sequences where attention’s quadratic complexity becomes prohibitive. Recent advances like Mamba [5] have shown how to make SSMs even more efficient with selective state spaces.
The Limitation
SSMs struggle with explicit context modeling - they can’t easily decide that a distant token is more important than a recent one based on semantic similarity. This limitation has been a key motivator for recent work like Mamba [5] and other SSM variants [6,7].
Our Proposed Solution: Context-Aware SSMs
We propose enhancing SSMs with a similarity mechanism inspired by attention. Instead of measuring similarity between current and past tokens (like attention does), we measure similarity between the current token and the current memory state:
$$g(x_i, h_{i-1}) = \sigma(x_i W_H h_{i-1}^T)$$
This similarity score then weights the input:
$$h_i = h_{i-1} A + x_i g(x_i, h_{i-1}) B$$
$$y_i = h_i C$$
The Intuition
Think of the memory state $h_{i-1}$ as containing a compressed representation of all past context. When a new token $x_i$ arrives, we check how well it “fits” with this accumulated context. Tokens that are highly relevant to the current context get stronger weights in the state update.
This is like having a conversation where you pay more attention to statements that connect well with the topic you’ve been discussing, while still maintaining a continuous thread of memory.
Dynamic System Properties
An important insight from our analysis concerns the stability properties of SSMs. The eigenvalues of matrix $A$ determine the model’s behavior:
- Stable systems (eigenvalues ≤ 1): Information fades gracefully over time
- Unstable systems (eigenvalues > 1): Information grows unboundedly, leading to numerical issues
- Oscillating systems (complex eigenvalues): Create periodic patterns in the output
For language modeling, we want stable, non-oscillating behavior. This constrains $A$ to have real, positive eigenvalues bounded by 1, which can be achieved using diagonal matrices with sigmoid-activated elements. This insight has been crucial for modern SSM architectures like S4 [3], Mamba [5], and other recent developments [8,9].
Looking Forward: Implementation Challenges
While theoretically elegant, our proposed context-aware SSM extension faces several practical challenges:
- Training Complexity: The nonlinear similarity term may complicate gradient-based optimization
- Vanishing Gradients: Like other recurrent models, SSMs can suffer from vanishing gradients over long sequences
- Computational Overhead: Adding similarity computation increases the computational cost
However, we believe the potential benefits - combining SSMs’ efficiency with attention’s context awareness - make this a promising research direction.
Conclusion
The relationship between attention mechanisms and state space models runs deeper than their surface-level differences suggest. Both are solving the same fundamental problem: how to selectively use past information for current predictions.
Attention prioritizes semantic relevance, while SSMs prioritize computational efficiency. Our work suggests that we don’t have to choose - by integrating attention-like similarity measures into SSMs, we may be able to achieve the best of both worlds.
As language models continue to handle longer and longer sequences, finding efficient ways to model context becomes increasingly critical. The marriage of attention and state space concepts may be key to building the next generation of language models that are both computationally efficient and contextually aware.
The journey from attention to state space models and back again reminds us that in machine learning, the most powerful solutions often come from understanding and combining different perspectives on the same underlying problem.
Link to the Paper
References
[1] Hrycej, T., Bermeitinger, B., & Handschuh, S. (2025). Integrating the Attention Mechanism into State Space Models. Proceedings of the 2025 IEEE Swiss Conference on Data Science (SDS) Url: ieeexplore.ieee.org/document/11081496.
[2] Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, L., & Polosukhin, I. (2017). Attention is all you need. Advances in neural information processing systems, 30, Url: arxiv.org/abs/1706.03762
[3] Gu, A., Goel, K., & Ré, C. (2021). Efficiently modeling long sequences with structured state spaces. arXiv preprint arXiv:2111.00396, Url: arxiv.org/abs/2111.00396
[4] Gu, A., Johnson, I., Goel, K., Saab, K., Dao, T., Rudra, A., & Ré, C. (2021). Combining recurrent, convolutional, and continuous-time models with linear state space layers. Advances in neural information processing systems, 34, Url: arxiv.org/abs/2110.13985
[5] Gu, A., & Dao, T. (2023). Mamba: Linear-time sequence modeling with selective state spaces. arXiv preprint arXiv:2312.00752, Url: arxiv.org/abs/2312.00752
[6] Dao, T., Fu, D., Ermon, S., Rudra, A., & Ré, C. (2022). FlashAttention: Fast and memory-efficient exact attention with IO-awareness. Advances in Neural Information Processing Systems, 35, arxiv.org/abs/2205.14135
[7] Sieber, J., Alonso, C. A., Didier, A., Zeilinger, M. N., & Orvieto, A. (2024). Understanding the differences in foundation models: Attention, state space models, and recurrent neural networks. arXiv preprint arXiv:2405.15731, Url: arxiv.org/abs/2405.15731
[8] Smith, J., Warrington, A., & Linderman, S. W. (2022). Simplified state space layers for sequence modeling. arXiv preprint arXiv:2208.04933, Url: arxiv.org/abs/2208.04933
[9] Mehta, H., Gupta, A., Cutkosky, A., & Neyshabur, B. (2022). Long range language modeling via gated state spaces. arXiv preprint arXiv:2206.13947, Url: arxiv.org/abs/2206.13947
